| Sujet : Graphe AT PRo : programmation |
| Page N° 43 | Sommaire des pages établi par LONGWAY et adapté par max-et-min Ce sommaire ne couvre pas la totalité des pages |
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonjour jlr,
Si tu places ta règle statistique à la fois sous les onglets JOUR et SEMAINE, il ne te donnera comme résultat que les actions qui satisfont à la fois les deux règles (voir doc GrapheAt Pro).
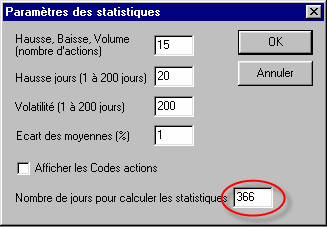
Il faut aussi vérifier que tu disposes d'assez de jours pour calculer la stat. Tu peux vérifier çà sous le bouton "Options" disponible dans la fenêtre "Statistiques" en haut.
Il faut un nombre de jour suffisant pour que çà marche :
Si tu places ta règle statistique à la fois sous les onglets JOUR et SEMAINE, il ne te donnera comme résultat que les actions qui satisfont à la fois les deux règles (voir doc GrapheAt Pro).
Il faut aussi vérifier que tu disposes d'assez de jours pour calculer la stat. Tu peux vérifier çà sous le bouton "Options" disponible dans la fenêtre "Statistiques" en haut.
Il faut un nombre de jour suffisant pour que çà marche :

|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
CONNAISSEZ-VOUS LA REGRESSION
NON-PARAMETRIQUE?
Les modèles classiques de régression sont paramétriques. Ils ne fournissent qu'une approximation, souvent limitée, de la structure sous-jacente des données auxquels ils sont appliqués.
Les modèles statistiques qui explicitent plus précisément les données sont souvent plus complexes que de simples polynômes fussent-ils trigonométriques ou autres (simple polynôme du 1er degré pour l'indicateur de régression linéaire REGLIN dans GrapheAT Pro par exemple).
A la différence de ces modèles, les méthodes de régression non-paramétriques consistent à estimer la relation liant les données sans faire la moindre hypothèse a priori sur la nature de cette liaison qui reste donc inconnue.
On doit surtout à Rosenblatt (1965), à Parzen (1962), à Cleveland(1979) et à bien d'autres la formalisation de cette approche. Son principe est très simple.
On définit une fenêtre glissante qui contient le point où on désire effectuer l'estimation. Ce point sera nommé point focal par la suite.
La taille de la fenêtre, dont le choix est laissé à l'utilisateur, influe fortement sur le résultat obtenu à l'instar de l'effet de la taille de la fenêtre glissante de calcul d'une moyenne mobile.
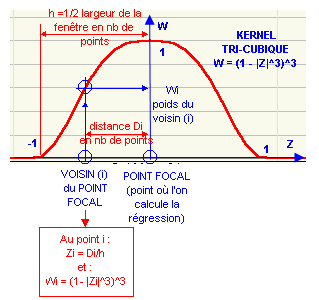
On choisit ensuite une fonction pondérante, ou noyau (kernel en anglais), des plus proches voisins de ce point qui sont contenus dans la fenêtre. La pondération dépend de la distance de ces voisins au point focal de telle sorte que les points éloignés du point focal soient affectés d'un poids moindre que les points qui en sont proches. Il existe une grande variété de fonctions pondérantes. Leur choix est peu influant sur le résultat final. On utilise souvent une fonction TRI-CUBIQUE définie comme suit .
Si Di est la distance du point focal au proche voisin i et h la 1/2 largeur de la fenêtre mobile centrée au point focal, en notant : Zi = Di/h cette distance relative, la pondération du voisin i est égale à :
Wi = (1 - |Zi|^3)^3 si Zi < 1 c'est à dire pour tout voisin i dans la fenêtre,
Wi = 0 si Zi >= 1 pour tous les points extérieurs à la fenêtre ou aux limites de celle-ci.
La méthode procède comme suit :
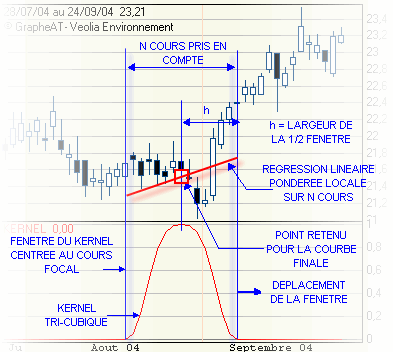
1- On positionne la fenêtre du kernel de telle sorte que son axe vertical soit sur le point focal c'est-à-dire centré sur le cours à partir duquel on souhaite calculer la régression.
2- On calcule les poids des voisins du point focal courant à l'aide de la fonction W ci-dessus définie.
3- On effectue ensuite une régression polynomiale locale sur les points i contenus dans la fenêtre et affectés des poids Wi. On utilise pour ce faire la méthode des moindres carrés.
Et on calcule la valeur de la régression au point focal qui donne l'estimation cherchée.
4- On déplace la fenêtre d'une période vers la droite.
5- On répète les pas précédents sur l'ensemble des points sur lesquels on souhaite calculer la régression non-paramétrique.
Ici, afin de simplifier les calculs nécessaires, nous choisirons un polynôme de degré 1 pour effectuer chaque régression locale pondérée. Cela permet en effet de calculer les paramètres de la droite de régression locale pondérée par la méthode des moindres carrés, pour chaque position de la fenêtre du kernel, sans avoir à manipuler de matrices (paramètres A, B, C, D, E, ALPHA et BETA dans le programme ci-dessous).
Les points obtenus dans les différentes fenêtres forment la courbe de régression cherchée.
Cette méthode s'apparente à la méthode LOWESS (LOcally WEighted Scatterplot Smoothing) de Cleveland qui comporte en plus des itérations de recherche de la robustesse du résultat obtenu dans le cas où des données seraient très éloignées des autres et risqueraient de fausser le résultat. Nous n'introduirons pas cette étape ici.
PROGRAMME :
--------------------------------------------------------------------------------------------------------
//REGRESSION NON-PARAMETRIQUE TYPE LOWESS
//V1.6 du 11/09/2004
//
//Calcul du nb de points dans la fenêtre de pondération
//et de la distance du bord au centre de la fenêtre
SI RANGHISTO=1
ALORS
SI MOD(ENTIER(P2*P3),2)=0
ALORS
N=ENTIER(P2*P3)+1
SINON
N=ENTIER(P2*P3)
FINSI
DMAXI= ENTIER(N/2)
FINSI
//Calcul de la régression locale et déplacement du kernel
//
SI RANGHISTO=FINHISTO-P1
ALORS
//Calcul des poids de proximité W(k) du kernel
//centré sur le point de départ
//
POUR (P2+DMAXI+1) COURS
W(0)=(1-(ABSOLU((-DMAXI-1+RANGPOUR)/DMAXI))^3)^3
W(2*((RANGPOUR-1)-DMAXI))=W(0)
SI RANGPOUR=(DMAXI+1) ALORS BREAK
FINPOUR
//Calcul de la régression locale
//
POUR (P2-DMAXI+1) COURS
POUR N COURS
X(0)=RANGPOUR
Y(0)=CLOTURE
FINPOUR
A=SOMME(W,N)
B=SOMME(W*X,N)
C=SOMME(W*Y,N)
D=SOMME(W*X*Y,N)
E=SOMME(W*X*X,N)
ALPHA=(A*D-B*C)/(A*E-B*B)
BETA=(C*E-B*D)/(A*E-B*B)
LOWESS(DMAXI)=ALPHA*X(DMAXI)+BETA
//Decalage de la fenêtre du kernel
//
SI RANGPOUR <=P2-DMAXI
ALORS
POUR N COURS
W(2*RANGPOUR-(N+2))=W(2*RANGPOUR-(N+1))
FINPOUR
FINSI
FINPOUR
//Traitement des derniers cas
//
J=1
TANTQUE J<=DMAXI FAIRE
//Déplacement fenêtre de pondération
POUR (N-J+1) COURS
W(2*RANGPOUR-(N-J+3))=W(2*RANGPOUR-(N-J+2))
FINPOUR
//Régression locale sur les derniers cas
POUR (N-J) COURS
X(0)=RANGPOUR
Y(0)=CLOTURE
FINPOUR
A=SOMME(W,N-J)
B=SOMME(W*X,N-J)
C=SOMME(W*Y,N-J)
D=SOMME(W*X*Y,N-J)
E=SOMME(W*X*X,N-J)
ALPHA=(A*D-B*C)/(A*E-B*B)
BETA=(C*E-B*D)/(A*E-B*B)
LOWESS(DMAXI-J)=ALPHA*X(DMAXI-J)+BETA
J=J+1
FINTANTQUE
FINSI
---------------------------------------------------------------------------------------------------
Fenêtre Propriétés :
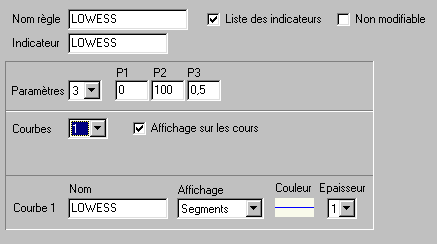
Le paramètre P1 fixe le cours de fin de la régression non-paramétrique.
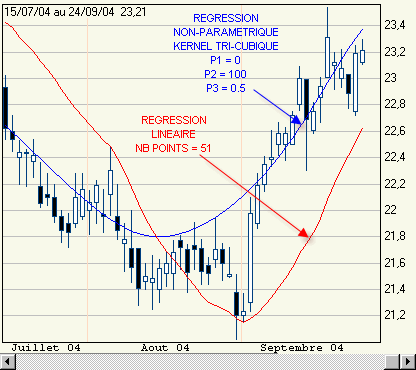
Si on souhaite la tracer jusqu'au dernier jour de l'historique, faire P1 = 0 comme ici.
Le paramètre P2 définit le nombre total de cours sur lesquels on souhaite calculer la régression avant P1 cours. Ici P2 = 100 cours.
P3 précise le ratio qui permet de déterminer combien la fenêtre glissante du kernel de pondération va contenir de cours. Ici P3 = 0.50, c'est-à-dire que la fenêtre glissante va contenir P2*P3 cours soit 100*0.50 = 50 cours. Ce nombre est transformé en nombre impair si nécessaire pour des raisons de calcul. On prendra 51 cours en l'occurence.
Afin d'illustrer ce que l'on obtient :
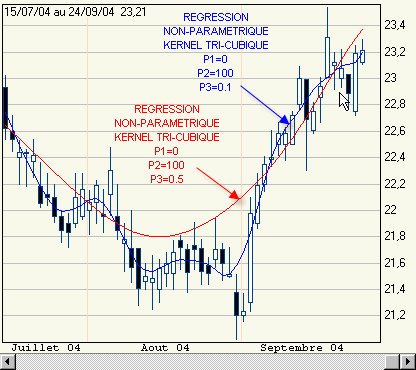
Comme on le constate ci-dessus où 2 courbes sont tracées avec des valeurs différentes du nombre de cours pris en compte, la largeur de la fenêtre du kernel de pondération a un effet important sur le résultat :
- si elle est trop petite (11 cours dans la fenêtre donnant la courbe bleue), il n'y a pas assez de données pour effectuer les calculs et le résultat est proche du point focal, la courbe obtenue au final est peu lissée, il y a peu de biais mais beaucoup de variance globale ;
- inversement si la largeur de la fenêtre est grande (51 cours pour la courbe rouge), il y a plus de données, le résultat est sur-lissé et éloigné des points réels, le biais est plus grand, la variance globale est plus faible que dans le cas précédent.
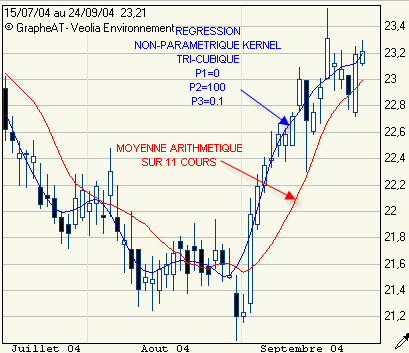
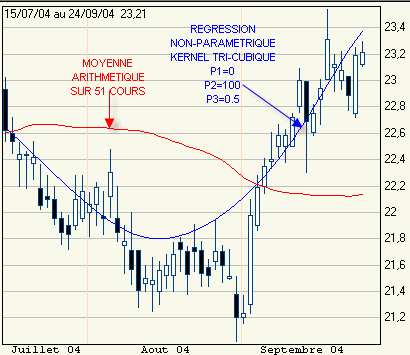
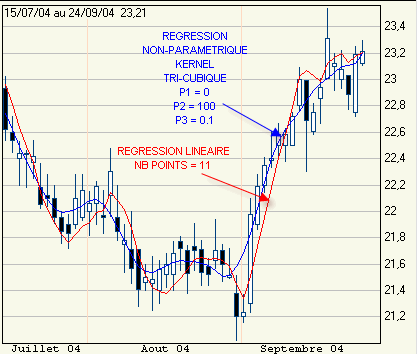
On obtient malgré tout des résultats qui semblent moins retardés qu'avec une simple moyenne mobile ou même qu'avec une classique régression paramétrique linéaire.
Les creux et les sommets sont atténués.
Vos impressions?
Les modèles classiques de régression sont paramétriques. Ils ne fournissent qu'une approximation, souvent limitée, de la structure sous-jacente des données auxquels ils sont appliqués.
Les modèles statistiques qui explicitent plus précisément les données sont souvent plus complexes que de simples polynômes fussent-ils trigonométriques ou autres (simple polynôme du 1er degré pour l'indicateur de régression linéaire REGLIN dans GrapheAT Pro par exemple).
A la différence de ces modèles, les méthodes de régression non-paramétriques consistent à estimer la relation liant les données sans faire la moindre hypothèse a priori sur la nature de cette liaison qui reste donc inconnue.
On doit surtout à Rosenblatt (1965), à Parzen (1962), à Cleveland(1979) et à bien d'autres la formalisation de cette approche. Son principe est très simple.
On définit une fenêtre glissante qui contient le point où on désire effectuer l'estimation. Ce point sera nommé point focal par la suite.
La taille de la fenêtre, dont le choix est laissé à l'utilisateur, influe fortement sur le résultat obtenu à l'instar de l'effet de la taille de la fenêtre glissante de calcul d'une moyenne mobile.
On choisit ensuite une fonction pondérante, ou noyau (kernel en anglais), des plus proches voisins de ce point qui sont contenus dans la fenêtre. La pondération dépend de la distance de ces voisins au point focal de telle sorte que les points éloignés du point focal soient affectés d'un poids moindre que les points qui en sont proches. Il existe une grande variété de fonctions pondérantes. Leur choix est peu influant sur le résultat final. On utilise souvent une fonction TRI-CUBIQUE définie comme suit .
Si Di est la distance du point focal au proche voisin i et h la 1/2 largeur de la fenêtre mobile centrée au point focal, en notant : Zi = Di/h cette distance relative, la pondération du voisin i est égale à :
Wi = (1 - |Zi|^3)^3 si Zi < 1 c'est à dire pour tout voisin i dans la fenêtre,
Wi = 0 si Zi >= 1 pour tous les points extérieurs à la fenêtre ou aux limites de celle-ci.

La méthode procède comme suit :
1- On positionne la fenêtre du kernel de telle sorte que son axe vertical soit sur le point focal c'est-à-dire centré sur le cours à partir duquel on souhaite calculer la régression.
2- On calcule les poids des voisins du point focal courant à l'aide de la fonction W ci-dessus définie.
3- On effectue ensuite une régression polynomiale locale sur les points i contenus dans la fenêtre et affectés des poids Wi. On utilise pour ce faire la méthode des moindres carrés.
Et on calcule la valeur de la régression au point focal qui donne l'estimation cherchée.
4- On déplace la fenêtre d'une période vers la droite.
5- On répète les pas précédents sur l'ensemble des points sur lesquels on souhaite calculer la régression non-paramétrique.

Ici, afin de simplifier les calculs nécessaires, nous choisirons un polynôme de degré 1 pour effectuer chaque régression locale pondérée. Cela permet en effet de calculer les paramètres de la droite de régression locale pondérée par la méthode des moindres carrés, pour chaque position de la fenêtre du kernel, sans avoir à manipuler de matrices (paramètres A, B, C, D, E, ALPHA et BETA dans le programme ci-dessous).
Les points obtenus dans les différentes fenêtres forment la courbe de régression cherchée.
Cette méthode s'apparente à la méthode LOWESS (LOcally WEighted Scatterplot Smoothing) de Cleveland qui comporte en plus des itérations de recherche de la robustesse du résultat obtenu dans le cas où des données seraient très éloignées des autres et risqueraient de fausser le résultat. Nous n'introduirons pas cette étape ici.
PROGRAMME :
--------------------------------------------------------------------------------------------------------
//REGRESSION NON-PARAMETRIQUE TYPE LOWESS
//V1.6 du 11/09/2004
//
//Calcul du nb de points dans la fenêtre de pondération
//et de la distance du bord au centre de la fenêtre
SI RANGHISTO=1
ALORS
SI MOD(ENTIER(P2*P3),2)=0
ALORS
N=ENTIER(P2*P3)+1
SINON
N=ENTIER(P2*P3)
FINSI
DMAXI= ENTIER(N/2)
FINSI
//Calcul de la régression locale et déplacement du kernel
//
SI RANGHISTO=FINHISTO-P1
ALORS
//Calcul des poids de proximité W(k) du kernel
//centré sur le point de départ
//
POUR (P2+DMAXI+1) COURS
W(0)=(1-(ABSOLU((-DMAXI-1+RANGPOUR)/DMAXI))^3)^3
W(2*((RANGPOUR-1)-DMAXI))=W(0)
SI RANGPOUR=(DMAXI+1) ALORS BREAK
FINPOUR
//Calcul de la régression locale
//
POUR (P2-DMAXI+1) COURS
POUR N COURS
X(0)=RANGPOUR
Y(0)=CLOTURE
FINPOUR
A=SOMME(W,N)
B=SOMME(W*X,N)
C=SOMME(W*Y,N)
D=SOMME(W*X*Y,N)
E=SOMME(W*X*X,N)
ALPHA=(A*D-B*C)/(A*E-B*B)
BETA=(C*E-B*D)/(A*E-B*B)
LOWESS(DMAXI)=ALPHA*X(DMAXI)+BETA
//Decalage de la fenêtre du kernel
//
SI RANGPOUR <=P2-DMAXI
ALORS
POUR N COURS
W(2*RANGPOUR-(N+2))=W(2*RANGPOUR-(N+1))
FINPOUR
FINSI
FINPOUR
//Traitement des derniers cas
//
J=1
TANTQUE J<=DMAXI FAIRE
//Déplacement fenêtre de pondération
POUR (N-J+1) COURS
W(2*RANGPOUR-(N-J+3))=W(2*RANGPOUR-(N-J+2))
FINPOUR
//Régression locale sur les derniers cas
POUR (N-J) COURS
X(0)=RANGPOUR
Y(0)=CLOTURE
FINPOUR
A=SOMME(W,N-J)
B=SOMME(W*X,N-J)
C=SOMME(W*Y,N-J)
D=SOMME(W*X*Y,N-J)
E=SOMME(W*X*X,N-J)
ALPHA=(A*D-B*C)/(A*E-B*B)
BETA=(C*E-B*D)/(A*E-B*B)
LOWESS(DMAXI-J)=ALPHA*X(DMAXI-J)+BETA
J=J+1
FINTANTQUE
FINSI
---------------------------------------------------------------------------------------------------
Fenêtre Propriétés :

Le paramètre P1 fixe le cours de fin de la régression non-paramétrique.
Si on souhaite la tracer jusqu'au dernier jour de l'historique, faire P1 = 0 comme ici.
Le paramètre P2 définit le nombre total de cours sur lesquels on souhaite calculer la régression avant P1 cours. Ici P2 = 100 cours.
P3 précise le ratio qui permet de déterminer combien la fenêtre glissante du kernel de pondération va contenir de cours. Ici P3 = 0.50, c'est-à-dire que la fenêtre glissante va contenir P2*P3 cours soit 100*0.50 = 50 cours. Ce nombre est transformé en nombre impair si nécessaire pour des raisons de calcul. On prendra 51 cours en l'occurence.
Afin d'illustrer ce que l'on obtient :

Comme on le constate ci-dessus où 2 courbes sont tracées avec des valeurs différentes du nombre de cours pris en compte, la largeur de la fenêtre du kernel de pondération a un effet important sur le résultat :
- si elle est trop petite (11 cours dans la fenêtre donnant la courbe bleue), il n'y a pas assez de données pour effectuer les calculs et le résultat est proche du point focal, la courbe obtenue au final est peu lissée, il y a peu de biais mais beaucoup de variance globale ;
- inversement si la largeur de la fenêtre est grande (51 cours pour la courbe rouge), il y a plus de données, le résultat est sur-lissé et éloigné des points réels, le biais est plus grand, la variance globale est plus faible que dans le cas précédent.
On obtient malgré tout des résultats qui semblent moins retardés qu'avec une simple moyenne mobile ou même qu'avec une classique régression paramétrique linéaire.
Les creux et les sommets sont atténués.




Vos impressions?
édité
le : 27-09-2004 11:05:30
|
|
FOKI
(2011
msg)
FOKI' style='text-decoration:none;'>PROFIL NON RENSEIGNÉ
Bonjour Smallcaps
Je viens de prendre connaissance de ton travail et je ne connaissais pas la "Légression non paramétrique" et pour cause je vais bientôt apprendre les divisions.
Je vais regarder cela de près et te donnerai mon avis, c'est le minimum qu'on te doit.
J'ai fait de mon coté des stats sur les Moyennes mobiles et sur la MamaFama avec l'aide du programme "Trade AchatVente" et "fenêtre affichage" dans graph AT. Je n'ai pas encore fini mais autant je n'ai pas réussi trouver un avantage avec MamaFama (mais c'est peut être de ma faute malgré bon nombre d'essais sur les paramétrages) autant l'utilisation des moyenne 20, 100 et 150 peuvent apporter quelques résultats (pas la fortune mais peuvent être un outil au trader) par leurs croisement .
.
FOKI
Je viens de prendre connaissance de ton travail et je ne connaissais pas la "Légression non paramétrique" et pour cause je vais bientôt apprendre les divisions.
Je vais regarder cela de près et te donnerai mon avis, c'est le minimum qu'on te doit.
J'ai fait de mon coté des stats sur les Moyennes mobiles et sur la MamaFama avec l'aide du programme "Trade AchatVente" et "fenêtre affichage" dans graph AT. Je n'ai pas encore fini mais autant je n'ai pas réussi trouver un avantage avec MamaFama (mais c'est peut être de ma faute malgré bon nombre d'essais sur les paramétrages) autant l'utilisation des moyenne 20, 100 et 150 peuvent apporter quelques résultats (pas la fortune mais peuvent être un outil au trader) par leurs croisement
FOKI
Laisser au marché,
nous donner la direction...
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Merci FOKI.
D'accord avec toi pour les X entre moyennes mobiles.
Mais encore faut-il trouver les bonnes valeurs de calcul pour profiter pleinement des périodes de tendance sans trop se faire pénaliser pendant les périodes de consolidation. Et là il y a peut-être mieux que 20,100 et 150 ?
D'accord avec toi pour les X entre moyennes mobiles.
Mais encore faut-il trouver les bonnes valeurs de calcul pour profiter pleinement des périodes de tendance sans trop se faire pénaliser pendant les périodes de consolidation. Et là il y a peut-être mieux que 20,100 et 150 ?
|
|
FOKI
(2011
msg)
FOKI' style='text-decoration:none;'>PROFIL NON RENSEIGNÉ
Pour Smallcaps
Pour utiliser cette methode, faut-il rechercher un système de croisement de 2 courbes (voir les paramétrages) pour passer les ordres ou bien une seule courbe peut suffir.
As tu déjà fait des essais ?
FOKI
Pour utiliser cette methode, faut-il rechercher un système de croisement de 2 courbes (voir les paramétrages) pour passer les ordres ou bien une seule courbe peut suffir.
As tu déjà fait des essais ?
FOKI
Laisser au marché, nous donner la direction...
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Non FOKI ce n'est pas une méthode
en soi, c'est un simple indicateur de filtrage des cours qui semble avoir moins
de lag que d'autres comme la regression paramétrique linéaire, les moyennes mobiles
et moins "heurté" que Kalman, Tema... pour des paramètres de calcul identiques.
|
|
pwaget
(534
msg)
pwaget' style='text-decoration:none;'>PROFIL NON RENSEIGNÉ
Une bonne adresse où trouver des
descriptifs de systèmes (très) avancés de trading : http://www.meyersanalytics.com/articles.php
Les équations mathématiques sont données, en les codant, cela permettra très certainement de faire avancer la réflexion de plusieurs bonds.
Meyer donne notamment une alternative plus efficace du système MESA.
Il faut noter que tous les articles sont en anglais et de haut niveau, mais le jeu en vaut la chandelle, les systèmes obtenus permettent d'avoir des taux de trades profitables proches des 60% et certains systèmes des "profit factor" proche de 3 !
Les équations mathématiques sont données, en les codant, cela permettra très certainement de faire avancer la réflexion de plusieurs bonds.
Meyer donne notamment une alternative plus efficace du système MESA.
Il faut noter que tous les articles sont en anglais et de haut niveau, mais le jeu en vaut la chandelle, les systèmes obtenus permettent d'avoir des taux de trades profitables proches des 60% et certains systèmes des "profit factor" proche de 3 !
édité le : 27-09-2004
18:39:21
|
|
sphinx
(91
msg) ![]()
![]()
![]()
![]()
je me sens totalement incompétent
pour donner un avis à Smallcaps. Mais le travail fourni est énorme.
Merci à Pwaget pour son lien meme' si je ne parle que très peu la langue d'outre manche.
Merci à Pwaget pour son lien meme' si je ne parle que très peu la langue d'outre manche.
|
|
jlr
(372
msg) ![]()
![]()
![]()
![]()
j'en reviens à mes pb de stat weekly,
juste pour remercier smallcaps, c'était la profondeur de recherche qui n'était
pas assez importante.
jlr
jlr
|
|
RickenBroc
(88
msg) ![]()
![]()
![]()
![]()
Bonjour Smallcaps90,
Intéressante, cette régréssion non paramétrique, mais pondérée.
Comme toute régression, il faut quand même se méfier, car la forme de la courbe change quand on avance dans le temps.
Par exemple sur carrefour au 17/09/2004 puis au 24/09/2004
On voit bien que la forme de la courbe a été modifiée dans le passé.
Alors, comment s'en servir au quotidien, voilà la question...
Cordialement,
RickenBroc
Intéressante, cette régréssion non paramétrique, mais pondérée.
Comme toute régression, il faut quand même se méfier, car la forme de la courbe change quand on avance dans le temps.
Par exemple sur carrefour au 17/09/2004 puis au 24/09/2004
On voit bien que la forme de la courbe a été modifiée dans le passé.
Alors, comment s'en servir au quotidien, voilà la question...
Cordialement,
RickenBroc
édité le : 28-09-2004
17:30:19et puis il y eu le Big Bang...
|
|
providence

(14121
msg) ![]()
![]()
![]()
![]()
D'après ce que j'ai compris les
régressions linéaires,comme les mme doivent s'utiliser en tradant dans le sens
que la courbe vient de prendre.
Quelqu'un en a-t-il une autre utilisation?
Quelqu'un en a-t-il une autre utilisation?
|
|
FOKI
(2011
msg)
FOKI' style='text-decoration:none;'>PROFIL NON RENSEIGNÉ
Bonjour Smallcaps
Je reviens vers toi pour savoir si tu as toujours en projet de faire le programme des divergences RSI et Stoch
Amicalement
FOKI
Je reviens vers toi pour savoir si tu as toujours en projet de faire le programme des divergences RSI et Stoch
Amicalement
FOKI
Laisser
au marché, nous donner la direction...
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonjour RickenBroc,
Effectivement, tu mets l'accent sur un vrai problème avec les regressions.
Il ne faut pas attendre de miracle.
Le problème que tu évoques est du au fait qu'en fin de calcul, le kernel n'est plus symétrique comme il l'était à l'intérieur du domaine exploré. Comme on le décale progressivement vers la droite, il arrive qu'en fin de parcours il n'en reste plus que la moitié gauche. On peut d'ailleurs ne conserver que cette moitié gauche pour la totalité du calcul. J'ai fait des essais pour voir ce que cela donne. Pas merveilleux....
Je sais par ailleurs que certains chercheurs ont proposé des méthodes pour améliorer le biais trop variable qu'on obtient à la limite droite du domaine de calcul. Cela nécessite une étude supplémentaire et une modification du programme. Je vais regarder çà.
On peut aussi réduire le paramètre P3 pour avoir un lissage moins important mais la courbe obtenue présentera toujours une mofication de sa forme lors d'un changement brutal de tendance, moindre cependant qu'avec un fort lissage.
Bien cordialement.
Effectivement, tu mets l'accent sur un vrai problème avec les regressions.
Il ne faut pas attendre de miracle.
Le problème que tu évoques est du au fait qu'en fin de calcul, le kernel n'est plus symétrique comme il l'était à l'intérieur du domaine exploré. Comme on le décale progressivement vers la droite, il arrive qu'en fin de parcours il n'en reste plus que la moitié gauche. On peut d'ailleurs ne conserver que cette moitié gauche pour la totalité du calcul. J'ai fait des essais pour voir ce que cela donne. Pas merveilleux....
Je sais par ailleurs que certains chercheurs ont proposé des méthodes pour améliorer le biais trop variable qu'on obtient à la limite droite du domaine de calcul. Cela nécessite une étude supplémentaire et une modification du programme. Je vais regarder çà.
On peut aussi réduire le paramètre P3 pour avoir un lissage moins important mais la courbe obtenue présentera toujours une mofication de sa forme lors d'un changement brutal de tendance, moindre cependant qu'avec un fort lissage.
Bien cordialement.
édité
le : 29-09-2004 12:01:37
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonjour FOKI,
Oui les programmes de détection des divergences cours/STOCH et cours/RSI sont opérationnels, ainsi que les stats correspondantes. Vu leurs longueurs, je ne pense pas que je les mettrai en ligne ici.
Si tu es intéressé je peux te les transmettre par email...
Cordialement.
Oui les programmes de détection des divergences cours/STOCH et cours/RSI sont opérationnels, ainsi que les stats correspondantes. Vu leurs longueurs, je ne pense pas que je les mettrai en ligne ici.
Si tu es intéressé je peux te les transmettre par email...
Cordialement.
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonjour,
Voici une petite "récréation".
A la demande de Philippulus, afin de visualiser les variations de la volatilité, il s'agissait de programmer pour l'A T D M F® (nom déposé par P Cahen), la réalisation d'une courbe de l'écart-type à 20 jours du cours moyen en coloriant en rouge ses parties descendantes et en vert ses parties montantes.
Pas très facile a priori, même avec le type de tracés "Segments" des courbes. En effet "Segment" ne trace pas les valeurs "0" et, de ce fait j'avais des discontinuités que je ne parvenais pas à supprimer dans les tracés entre les parties vertes et rouges.
La solution proposée ici consiste à créer pour chaque segment de courbe deux sous-segments : ECR1 et ECR2 pour les segments rouges, ECV1 et ECV2 pour les segments verts, et à alterner leur tracé en utilisant la séquence : ...., ECR1, ECV1, ECR2, ECV2, ECR1,.....
Ainsi les vides entre les sous-segments sont comblés.
Si vous trouvez une autre solution, je suis preneur...
PROGRAMME :
-----------------------------------------------------------------------------------------
//Ecart-Type coloré du cours moyen à P1=20 jours pour A T D M F® (nom déposé par P Cahen)
//
//1- Calcul écart-type du cours moyen
C_MOYEN(0)=(HAUT+BAS+CLOTURE)/3
EC = ECARTYPE(C_MOYEN,P1)
//2- Initialisations
SI RANGHISTO=2
ALORS
SI EC>=EC(1)
ALORS
V(0)=1
R(0)=0
SINON
V(0)=0
R(0)=1
FINSI
FINSI
SI RANGHISTO>2
ALORS
//3- Détermination de la tendance
SI EC(1)>EC
ALORS
R=1
V=0
FINSI
SI EC(1)<EC
ALORS
V=1
R=0
FINSI
SI EC(1)=EC
ALORS
SI V(1)=1 ALORS V=V(1)
SI R(1)=1 ALORS R=R(1)
FINSI
//Traitement des tracés
//
//Pour les segments verts
//
SI V=1 ET V(1)=0
ALORS
SI A=0
ALORS
ECV1(1)=EC(1)
ECV1=EC
SINON
ECV2(1)=EC(1)
ECV2=EC
FINSI
FINSI
SI V=1 ET V(1)=1
ALORS
SI A=0 ALORS ECV1=EC
SI A=1 ALORS ECV2=EC
FINSI
SI V=0 ET V(1)=1
ALORS
SI A=0 ALORS ECV1(1)=EC(1)
SI A=1 ALORS ECV2(1)=EC(1)
A=NON(A)
FINSI
//Pour les segments rouges
//
SI R=1 ET R(1)=0
ALORS
SI B=0
ALORS
ECR1(1)=EC(1)
ECR1=EC
SINON
ECR2(1)=EC(1)
ECR2=EC
FINSI
FINSI
SI R=1 ET R(1)=1
ALORS
SI B=0 ALORS ECR1=EC
SI B=1 ALORS ECR2=EC
FINSI
SI R=0 ET R(1)=1
ALORS
SI B=0 ALORS ECR1(1)=EC(1)
SI B=1 ALORS ECR2(1)=EC(1)
B=NON(B)
FINSI
FINSI
-----------------------------------------------------------------------------------------
Fenêtre PROPRIETES :
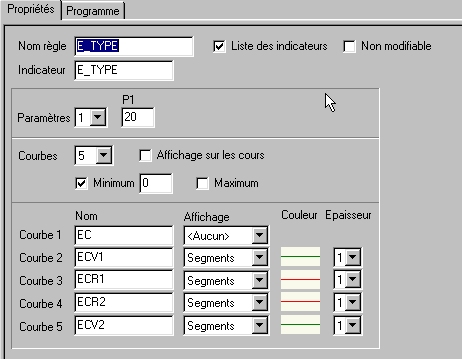
Un exemple :
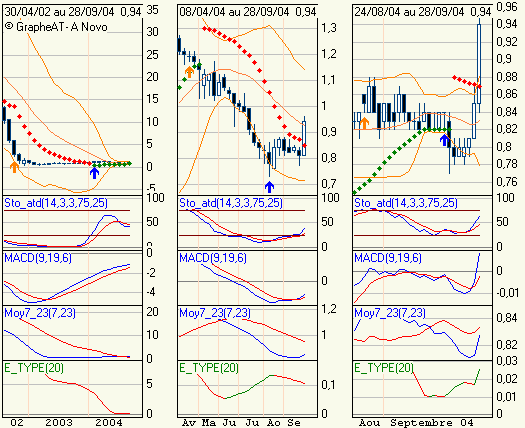
Voici une petite "récréation".
A la demande de Philippulus, afin de visualiser les variations de la volatilité, il s'agissait de programmer pour l'A T D M F® (nom déposé par P Cahen), la réalisation d'une courbe de l'écart-type à 20 jours du cours moyen en coloriant en rouge ses parties descendantes et en vert ses parties montantes.
Pas très facile a priori, même avec le type de tracés "Segments" des courbes. En effet "Segment" ne trace pas les valeurs "0" et, de ce fait j'avais des discontinuités que je ne parvenais pas à supprimer dans les tracés entre les parties vertes et rouges.
La solution proposée ici consiste à créer pour chaque segment de courbe deux sous-segments : ECR1 et ECR2 pour les segments rouges, ECV1 et ECV2 pour les segments verts, et à alterner leur tracé en utilisant la séquence : ...., ECR1, ECV1, ECR2, ECV2, ECR1,.....
Ainsi les vides entre les sous-segments sont comblés.
Si vous trouvez une autre solution, je suis preneur...
PROGRAMME :
-----------------------------------------------------------------------------------------
//Ecart-Type coloré du cours moyen à P1=20 jours pour A T D M F® (nom déposé par P Cahen)
//
//1- Calcul écart-type du cours moyen
C_MOYEN(0)=(HAUT+BAS+CLOTURE)/3
EC = ECARTYPE(C_MOYEN,P1)
//2- Initialisations
SI RANGHISTO=2
ALORS
SI EC>=EC(1)
ALORS
V(0)=1
R(0)=0
SINON
V(0)=0
R(0)=1
FINSI
FINSI
SI RANGHISTO>2
ALORS
//3- Détermination de la tendance
SI EC(1)>EC
ALORS
R=1
V=0
FINSI
SI EC(1)<EC
ALORS
V=1
R=0
FINSI
SI EC(1)=EC
ALORS
SI V(1)=1 ALORS V=V(1)
SI R(1)=1 ALORS R=R(1)
FINSI
//Traitement des tracés
//
//Pour les segments verts
//
SI V=1 ET V(1)=0
ALORS
SI A=0
ALORS
ECV1(1)=EC(1)
ECV1=EC
SINON
ECV2(1)=EC(1)
ECV2=EC
FINSI
FINSI
SI V=1 ET V(1)=1
ALORS
SI A=0 ALORS ECV1=EC
SI A=1 ALORS ECV2=EC
FINSI
SI V=0 ET V(1)=1
ALORS
SI A=0 ALORS ECV1(1)=EC(1)
SI A=1 ALORS ECV2(1)=EC(1)
A=NON(A)
FINSI
//Pour les segments rouges
//
SI R=1 ET R(1)=0
ALORS
SI B=0
ALORS
ECR1(1)=EC(1)
ECR1=EC
SINON
ECR2(1)=EC(1)
ECR2=EC
FINSI
FINSI
SI R=1 ET R(1)=1
ALORS
SI B=0 ALORS ECR1=EC
SI B=1 ALORS ECR2=EC
FINSI
SI R=0 ET R(1)=1
ALORS
SI B=0 ALORS ECR1(1)=EC(1)
SI B=1 ALORS ECR2(1)=EC(1)
B=NON(B)
FINSI
FINSI
-----------------------------------------------------------------------------------------
Fenêtre PROPRIETES :

Un exemple :

édité
le : 29-09-2004 16:16:14
|
|
43
| Sujet : Graphe AT PRo : programmation |