| Sujet : Graphe AT PRo : programmation |
| Page N° 15 | Sommaire des pages établi par LONGWAY et adapté par max-et-min Ce sommaire ne couvre pas la totalité des pages |
oxythan
(706
msg)
citation :
Citation de smallcaps90
Bonsoir Oxythan.
Tu me prends un peu au dépourvu, je n'ai pas vraiment réfléchi au nom à donner à la variante que j'ai proposée et qui n'est, je tiens à le répéter, qu'une prolongation de ton travail.
Je vais y réfléchir.
Bonne soirée.
prolongation et j'espère amélioration...
la pérénité d'un indicateur m'interesse moins que sa performance, aussi si tu l'améliore j'ai un grand intéret a tenir compte des variantes que tu aura proposé.
Je suis en train de faire ( pendant mes congés maladie ) un programme sur GraphATPro pourle backtester. dès que ça marche je te l'envois, on pourra ainsi vite tester l'efficassité des améliorations.
David.
Les p?riodes
sombres regorgent de proph?tes.
Precurseur de volatilit?: forums/topic.asp?TOPIC_ID=10...
Precurseur de volatilit?: forums/topic.asp?TOPIC_ID=10...
|
|
augusseau
(178
msg) ![]()
![]()
![]()
![]()
slt smallcaps,
je suis tres interressé par ton indicateur.
j'utilise altistock.
pourrais tu préciser à quoi correspond ranghisto, finhisto et les différents tests qui en découlent???
je suis tres interressé par ton indicateur.
j'utilise altistock.
pourrais tu préciser à quoi correspond ranghisto, finhisto et les différents tests qui en découlent???
carca
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonjour Augusseau.
Avec GrapheAT Pro, la variable RANGHISTO correspond au numéro du jour courant de l'historique sur lequel s'exécute le programme. Le 1er jour de l'historique a pour valeur de RANGHISTO, 1.
Dans une répétitive "POUR", RANGHISTO contient le jour courant de l'itération.
La variable FINHISTO au nombre total de jours dans l'historique.
Quant aux différents tests présents dans le programme, ils correspondent aux différentes parties de l'algorithme.
Je pense que çà ne devrait pas te poser beaucoup de problème à programmer avec Altistock.
Si tu le souhaites néanmoins, je peux t'envoer le code en pseudo-langage.
Avec GrapheAT Pro, la variable RANGHISTO correspond au numéro du jour courant de l'historique sur lequel s'exécute le programme. Le 1er jour de l'historique a pour valeur de RANGHISTO, 1.
Dans une répétitive "POUR", RANGHISTO contient le jour courant de l'itération.
La variable FINHISTO au nombre total de jours dans l'historique.
Quant aux différents tests présents dans le programme, ils correspondent aux différentes parties de l'algorithme.
Je pense que çà ne devrait pas te poser beaucoup de problème à programmer avec Altistock.
Si tu le souhaites néanmoins, je peux t'envoer le code en pseudo-langage.
|
|
augusseau
(178
msg) ![]()
![]()
![]()
![]()
slt smallcaps
si tu peux m'envoyer le code en pseudolangage je suis preneur.
en attendant j'ai programmé l'indicateur d'oxythan.
au-delà de l'accroissement de la volatilité, il me semble qu'on peut observer quelques regles de comportement :
- lorsque la volatilité croit, mais que le volatprcecurseur a fait un croisement bien en amont dans le temps, ou bien en dessous du zéro, le mouvement a peu de chance d'aller loin (demibulle)
- lorsque la volatilité croit et que le volatilprécurseur était proche du zéro et quasiment plat alors on aura un beau décallage...
voila pour mes qq observations.
je pense qu'on peut en trouver d'autres.
il s'agit effectivement d'un voie de recherche importante pour savoir ce que l'on va rencontrer (bulle, demi bulle...)
bon merci d'avance si tu m'envoies le code
si tu peux m'envoyer le code en pseudolangage je suis preneur.
en attendant j'ai programmé l'indicateur d'oxythan.
au-delà de l'accroissement de la volatilité, il me semble qu'on peut observer quelques regles de comportement :
- lorsque la volatilité croit, mais que le volatprcecurseur a fait un croisement bien en amont dans le temps, ou bien en dessous du zéro, le mouvement a peu de chance d'aller loin (demibulle)
- lorsque la volatilité croit et que le volatilprécurseur était proche du zéro et quasiment plat alors on aura un beau décallage...
voila pour mes qq observations.
je pense qu'on peut en trouver d'autres.
il s'agit effectivement d'un voie de recherche importante pour savoir ce que l'on va rencontrer (bulle, demi bulle...)
bon merci d'avance si tu m'envoies le code
carca
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Rebonsoir Augusseau.
Tout à fait d'accord avec toi. Il est normal que lorsque la dérivée augmente vite après un croisement positif predicteur/signal, cela veut dire que la volatilité croît très vite et donc que le mouvement risque de s'essouffler non moins vite (bulle/demi-bulle). Alors que si elle augmente lentement, la volatilité va faire de même et on aura peut-être la chance d'avoir des //. Même chose quant à la position du prédicteur et de son signal par rapport à la ligne 0 et à leurs formes également plus ou moins étalée comme tu l'as bien remarqué, prédicteur et signal qui ne sont, ne l'oublions pas, qu'un lissage (efficce mais sans retard!!!) de cette même dérivée.
A la demande bien compréhensible d'Oxythan j'ai modifié le nom de l'indicateur que je propose.
Il se nomme dorénavant : “SLOPE VOLATILITY PREDICTOR”
Comme promis tantôt, voici le code en pseudo-langage qui devrait te permettre de programmer le prédicteur sur Altistock ou tout autre système. Code à adapter bien sûr...
------------------------
CODE “SLOPE VOLATILITY PREDICTOR”
PSEUDO-LANGAGE
REMARQUES PRELIMINAIRES :
On notera (n+1) le nombre de périodes de cotation dans l’historique.
La première période est repèrée par i=0, la dernière par i=n.
Les (n+1) périodes de cotation sont également espacées dans le temps dans l’historique concerné.
Il y a n intervalles entre ces périodes de cotation dans l’historique concerné.
Chaque segment de spline cubique entre deux périodes de cotation successives a comme équation :
SPj(t) = A(j) + B(j)*(t-tj) + C(j)*(t-tj)^2 + D(j)*(t-tj)^3
Où j, variant de 0 à (n-1), représente la période de cotation courante, à gauche du segment considéré.
On notera EMA(X,T) la moyenne exponentielle de X sur la durée T.
On utilisera les notations propres à l’ATDMF pour désigner les bandes et la moyenne de Bollinger.
// Précèdera un commentaire
ALGORITHME :
//1- Calculer la volatilité relative des cours :
POUR chaque période de cotation
FAIRE //i varie donc de 0 à n
VOL(i) = 100*(UB(i) – LB(i)) / MB(i)
FIN FAIRE
FIN POUR
//2- Calculer les coefficients A(i), B(i), C(i) et D(i) de la spline cubique libre
// qui interpole la volatilité relative.
//
// Les A(i) ne sont pas indispensables à connaître pour calculer la dérivée première de la spline.
//Néanmoins les A(i) sont = VOL(i).
POUR chaque période de cotation de la première à l’avant dernière //i varie donc de 0 à( n-1)
FAIRE
ALPHA(i) = 3*(VOL(i+1) – 2*VOL(i) + VOL(i-1))
FIN FAIRE
FIN POUR
FAIRE
L(0) = 1
U(0) = 0
Z(0) = 0
FIN FAIRE
POUR chaque période de cotation de la deuxième à l’avant dernière //i varie donc de 1 à (n-1)
FAIRE
L(i) = 4 – U(i-1)
U(i) = 1 / L(i)
Z(i) = (ALPHA(i) – Z(i-1)) / L(i)
FIN FAIRE
FIN POUR
FAIRE
L(n) = 1
Z(n) = 0
C(n) = 0
FIN FAIRE
// Rétropropagation
POUR chaque période de cotation de l’avant-dernière à la première //j varie donc de (n-1) à 0
FAIRE
C(j) = Z(j) – U(j)*C(j+1)
B(j) = (VOL(j+1) – VOL(j)) – (C(j+1) + 2*C(j)) / 3
D(j) = (C(j+1) – C(j)) / 3
FIN FAIRE
FIN POUR
//3- Calculer la dérivée première de la spline qui est l’approximation de la pente de la tangente en chaque période //de cotation.
// Et éventuellement la dérivée seconde qui en représente la courbure (mise en commentaire ici).
POUR chaque période de cotation de la première à l’avant dernière //i varie donc de 0 à (n-1)
FAIRE
DERIVEEPREMIERE(i) = B(i)
//DERIVEESECONDE(i) = 2*C(i)
FIN FAIRE
FIN POUR
//Calculer les dérivées à la dernière période de cotation n.
FAIRE
DERIVEEPREMIERE(n) = B(n) + 2*C(n) + 3*D(n)
//DERIVEESECONDE(i) = 2*C(n) + 6*D(n)
FIN FAIRE
//4- Calculer le momentum à une période de la dérivée première.
//Lisser ce momentum à l’aide de 3 moyennes exponentielles de paramètres P1, P2, P3.
//Calculer la dérivée première lissée et son signal (moyenne exponentielle de paramètre P4)
POUR chaque période de cotation //i varie donc de 0 à n
FAIRE MOMENTUM(i) = DERIVEEPREMIERE(i) – DERIVEEPREMIERE(i-1)
M1(i) = EMA(MOMENTUM(i),P1)
M2(i) = EMA(M1(i),P2)
M3(i) = EMA(M2(i),P3)
ABSMOM(i) = VALEUR ABSOLUE(MOMENTUM(i))
M4(i) = EMA(ABSMOM(i),P1)
M5(i) = EMA(M4(i),P2)
M6(i) = EMA(M5(i),P3)
DERIVEEPREMIERELISSEE(i) = 100*M3(i) / M6(i)
SIGNAL(i) = EMA(DERIVEEPREMIERELISSEE(i),P4)
FIN FAIRE
FIN POUR
//5-Tracer les graphes de VOL, DERIVEEPREMIERE, DERIVEEPREMIERELISSEE et SIGNAL--------------------------------------
J'ai également glissé l'expression de la dérivée seconde dans le programme. Celle-ci représente la courbure de la volatilité...qui sait, cela pourra peut-être donner des idées à quelqu'un....
Bonne soirée et bon courage
----------------------------------------
Correction du 22 mars 2004.
Mes excuses à ceux d'entre-vous qui ont utilisé ce pseudo-code pour le traduire dans leur langage préféré.
En effet une petite erreur s'est glissée dans la formule donnant la valeur du paramètre ALPHA :
- le facteur 3 intervient sur l'ensemble du 2ème membre comme il est indiqué dans la ligne que j'ai marquée en rouge ci-dessus.
Le listing de l'indicateur dans GrapheAT PRO par contre est correct.
Merci à NACBIS qui m'a signalé cette erreur.
----------------------------------------
Tout à fait d'accord avec toi. Il est normal que lorsque la dérivée augmente vite après un croisement positif predicteur/signal, cela veut dire que la volatilité croît très vite et donc que le mouvement risque de s'essouffler non moins vite (bulle/demi-bulle). Alors que si elle augmente lentement, la volatilité va faire de même et on aura peut-être la chance d'avoir des //. Même chose quant à la position du prédicteur et de son signal par rapport à la ligne 0 et à leurs formes également plus ou moins étalée comme tu l'as bien remarqué, prédicteur et signal qui ne sont, ne l'oublions pas, qu'un lissage (efficce mais sans retard!!!) de cette même dérivée.
A la demande bien compréhensible d'Oxythan j'ai modifié le nom de l'indicateur que je propose.
Il se nomme dorénavant : “SLOPE VOLATILITY PREDICTOR”
Comme promis tantôt, voici le code en pseudo-langage qui devrait te permettre de programmer le prédicteur sur Altistock ou tout autre système. Code à adapter bien sûr...
------------------------
CODE “SLOPE VOLATILITY PREDICTOR”
PSEUDO-LANGAGE
REMARQUES PRELIMINAIRES :
On notera (n+1) le nombre de périodes de cotation dans l’historique.
La première période est repèrée par i=0, la dernière par i=n.
Les (n+1) périodes de cotation sont également espacées dans le temps dans l’historique concerné.
Il y a n intervalles entre ces périodes de cotation dans l’historique concerné.
Chaque segment de spline cubique entre deux périodes de cotation successives a comme équation :
SPj(t) = A(j) + B(j)*(t-tj) + C(j)*(t-tj)^2 + D(j)*(t-tj)^3
Où j, variant de 0 à (n-1), représente la période de cotation courante, à gauche du segment considéré.
On notera EMA(X,T) la moyenne exponentielle de X sur la durée T.
On utilisera les notations propres à l’ATDMF pour désigner les bandes et la moyenne de Bollinger.
// Précèdera un commentaire
ALGORITHME :
//1- Calculer la volatilité relative des cours :
POUR chaque période de cotation
FAIRE //i varie donc de 0 à n
VOL(i) = 100*(UB(i) – LB(i)) / MB(i)
FIN FAIRE
FIN POUR
//2- Calculer les coefficients A(i), B(i), C(i) et D(i) de la spline cubique libre
// qui interpole la volatilité relative.
//
// Les A(i) ne sont pas indispensables à connaître pour calculer la dérivée première de la spline.
//Néanmoins les A(i) sont = VOL(i).
POUR chaque période de cotation de la première à l’avant dernière //i varie donc de 0 à( n-1)
FAIRE
ALPHA(i) = 3*(VOL(i+1) – 2*VOL(i) + VOL(i-1))
FIN FAIRE
FIN POUR
FAIRE
L(0) = 1
U(0) = 0
Z(0) = 0
FIN FAIRE
POUR chaque période de cotation de la deuxième à l’avant dernière //i varie donc de 1 à (n-1)
FAIRE
L(i) = 4 – U(i-1)
U(i) = 1 / L(i)
Z(i) = (ALPHA(i) – Z(i-1)) / L(i)
FIN FAIRE
FIN POUR
FAIRE
L(n) = 1
Z(n) = 0
C(n) = 0
FIN FAIRE
// Rétropropagation
POUR chaque période de cotation de l’avant-dernière à la première //j varie donc de (n-1) à 0
FAIRE
C(j) = Z(j) – U(j)*C(j+1)
B(j) = (VOL(j+1) – VOL(j)) – (C(j+1) + 2*C(j)) / 3
D(j) = (C(j+1) – C(j)) / 3
FIN FAIRE
FIN POUR
//3- Calculer la dérivée première de la spline qui est l’approximation de la pente de la tangente en chaque période //de cotation.
// Et éventuellement la dérivée seconde qui en représente la courbure (mise en commentaire ici).
POUR chaque période de cotation de la première à l’avant dernière //i varie donc de 0 à (n-1)
FAIRE
DERIVEEPREMIERE(i) = B(i)
//DERIVEESECONDE(i) = 2*C(i)
FIN FAIRE
FIN POUR
//Calculer les dérivées à la dernière période de cotation n.
FAIRE
DERIVEEPREMIERE(n) = B(n) + 2*C(n) + 3*D(n)
//DERIVEESECONDE(i) = 2*C(n) + 6*D(n)
FIN FAIRE
//4- Calculer le momentum à une période de la dérivée première.
//Lisser ce momentum à l’aide de 3 moyennes exponentielles de paramètres P1, P2, P3.
//Calculer la dérivée première lissée et son signal (moyenne exponentielle de paramètre P4)
POUR chaque période de cotation //i varie donc de 0 à n
FAIRE MOMENTUM(i) = DERIVEEPREMIERE(i) – DERIVEEPREMIERE(i-1)
M1(i) = EMA(MOMENTUM(i),P1)
M2(i) = EMA(M1(i),P2)
M3(i) = EMA(M2(i),P3)
ABSMOM(i) = VALEUR ABSOLUE(MOMENTUM(i))
M4(i) = EMA(ABSMOM(i),P1)
M5(i) = EMA(M4(i),P2)
M6(i) = EMA(M5(i),P3)
DERIVEEPREMIERELISSEE(i) = 100*M3(i) / M6(i)
SIGNAL(i) = EMA(DERIVEEPREMIERELISSEE(i),P4)
FIN FAIRE
FIN POUR
//5-Tracer les graphes de VOL, DERIVEEPREMIERE, DERIVEEPREMIERELISSEE et SIGNAL--------------------------------------
J'ai également glissé l'expression de la dérivée seconde dans le programme. Celle-ci représente la courbure de la volatilité...qui sait, cela pourra peut-être donner des idées à quelqu'un....
Bonne soirée et bon courage
----------------------------------------
Correction du 22 mars 2004.
Mes excuses à ceux d'entre-vous qui ont utilisé ce pseudo-code pour le traduire dans leur langage préféré.
En effet une petite erreur s'est glissée dans la formule donnant la valeur du paramètre ALPHA :
- le facteur 3 intervient sur l'ensemble du 2ème membre comme il est indiqué dans la ligne que j'ai marquée en rouge ci-dessus.
Le listing de l'indicateur dans GrapheAT PRO par contre est correct.
Merci à NACBIS qui m'a signalé cette erreur.
----------------------------------------
édité le : 22-03-2004 11:58:40
|
|
augusseau
(178
msg) ![]()
![]()
![]()
![]()
slt smallcaps
je te remercie pour le code, je comprends mieux.
bon je vais regarder ce qu'on peut en tirer, et je te tiendrais au courant.
je te remercie pour le code, je comprends mieux.
bon je vais regarder ce qu'on peut en tirer, et je te tiendrais au courant.
carca
|
|
Nacbis
(961
msg) ![]()
![]()
![]()
![]()
Slope Volatility Predictor pour Platinium 5.00075
Ce fût plutôt difficile, car le langage de Platinium ne calcule pas correctement l’expression
ALPHA(0)=3*( VOL(-1) - 2*VOL(0) + VOL(1) )
Il faut décomposer
TOTO(0) = ( VOL(-1) + VOL(1) )
ALPHA(0)=3*(TOTO(0) - 2*VOL(0) )
Le temps de trouver …… Pffffffffffffffff
En conséquence, le code est très décomposé, pas très joli, m’enfin.
J’ai mis le code de Smallcaps dans une bibliothèque pour ne l’écrire qu’une fois.
Il faut ensuite créer des indicateurs dynamiques faisant appel à cette bibliothèque pour chaque courbe à dessiner, du genre
IncludeLib "1215331053:Slope Volatility Predictor"
Result = SVP(TBChart(), 0)
Attention, la ligne IncludeLib "1215331053:Slope Volatility Predictor" sera à remplacer par les références de votre bibliothèque qui n’aura pas les mêmes n°/nom.
Le 0 dans la ligne Result = SVP(TBChart(), 0) précise la courbe à dessiner (voir en fin de bibliothèque). Mettre de 0 à 3 selon la courbe souhaitée. C’est le seul truc un peu élégant, une seule fonction sort plusieurs courbes.
/////////////////////////////// DEBUT BIBLIOTHEQUE ///////////////////////////////////////////////////
function SVP( ZBC as variant, Indic as Integer ) as variant
dim ZTaille as integer ' Taille de l'historique de cours
dim ZTP as variant ' Typical Price
dim ZET as variant ' Ecart Type
dim ZMB as variant ' Moyenne de Bollinger
dim ZBWI as variant ' Bandwidth J. Bollinger ou volatilité normalisée P. Cahen
dim K as integer ' Compteur de boucle
dim ZCalc, ZCalc2, ZCalc3 as Double ' Calcul intermédiaire
dim ZResultat as variant
dim L, U, Z, C, B, D as variant
dim Alpha as variant
dim FPRIME4 as variant
dim DERIVEE1LISSEE as variant
dim FSECONDE4 as variant
dim ZMOMENTUM, ZMMT as variant
dim Signal as variant
dim MM1, MM2, MM3, MM4, MM5, MM6 as variant
' Intialisation des variants
ZResultat = ZBC - ZBC
ZTP = ZResultat
ZET = ZResultat
ZMB = ZResultat
ZBWI = ZResultat
Alpha = ZResultat
L = ZResultat
U = ZResultat
Z = ZResultat
C = ZResultat
B = ZResultat
D = ZResultat
FPRIME4 = ZResultat
FSECONDE4 = ZResultat
Signal = ZResultat
ZMomentum = ZResultat
ZMMT = ZResultat
MM1 = ZResultat
MM2 = ZResultat
MM3 = ZResultat
MM4 = ZResultat
MM5 = ZResultat
MM6 = ZResultat
DERIVEE1LISSEE = ZResultat
' Kalkulations
ZTaille = TailleTD(ZBC) ' Longueur de l'historique
ZTP = TTypPrice(ZBC) ' Typical Price
ZET = TSD(ZTP, 20 ) ' Ecart Type
ZMB = TMMA(ZTP, 20 ) ' Moyenne de Bollinger
ZBWI = (400 * ZET) / ZMB ' Bandwidth J. Bollinger ou volatilité normalisée P. Cahen
'2- Calculer les coefficients A(i), B(i), C(i) et D(i) de la spline cubique libre qui interpole la volatilité relative.
' Les A(i) ne sont pas indispensables à connaître pour calculer la dérivée première de la spline.
' Néanmoins les A(i) sont = VOL(i).
' POUR chaque période de cotation de la première à l'avant dernière //i varie donc de 0 à( n-1)
' ALPHA(i) = 3*VOL(i+1) - 2*VOL(i) + VOL(i-1)
L = TRef(ZBWI,-1)
Z = TRef(ZBWI,+1)
ZResultat = L+Z
Alpha = 3*( ZResultat - 2*ZBWI )
FixeElemTD(L, 1 , 0)
FixeElemTD(U, 1 , 0)
FixeElemTD(Z, 1 , 0)
For K = 2 to (ZTaille-1) ' dans Platinium K=1 désigne le cours le plus ancien
ZCalc = ( 4 - ValeurElemTD(U,(K-1)) )
FixeElemTD(L , K , ZCalc )
ZCalc2 = ( 1 / ZCalc )
FixeElemTD(U , K , ZCalc2 )
ZCalc2 = ( ValeurElemTD(Alpha, K) - ValeurElemTD(Z,(K-1)) )
ZCalc3 = ( ZCalc2 / ZCalc )
FixeElemTD(Z , K , ZCalc3 )
Next
FixeElemTD(L, ZTaille , 1)
FixeElemTD(Z, ZTaille , 0)
FixeElemTD(C, ZTaille , ValeurElemTD(Z,ZTaille) )
' Rétropropagation
' Pour chaque période de cotation de l'avant-dernière à la première //j varie donc de (n-1) à 0
' C(j) = Z(j) - U(j)*C(j+1)
' B(j) = (VOL(j+1) - VOL(j)) - (C(j+1) + 2*C(j)) / 3
' D(j) = (C(j+1) - C(j)) / 3
For K = (ZTaille-1) to 1 step -1
ZCalc = ( ValeurElemTD(U , K) * ValeurElemTD(C, K+1) )
ZCalc2 = ( ValeurElemTD(Z , K ) - ZCalc )
FixeElemTD(C , K , ZCalc2 )
ZCalc = ( ValeurElemTD(ZBWI, K+1) - ValeurElemTD(ZBWI, K) )
ZCalc2 = ( ( ValeurElemTD(C, K+1) + 2*ValeurElemTD(C, K) )/3 )
ZCalc3 = ZCalc - ZCalc2
FixeElemTD(B , K , ZCalc3 )
ZCalc = ( ValeurElemTD(C, K+1) - ValeurElemTD(C, K) )
ZCalc2 = ( ZCalc / 3 )
FixeElemTD(D , K , ZCalc2 )
Next
' 3- Calculer la dérivée première de la spline qui est l'approximation de la pente de la tangente en chaque période //de cotation.
' Et éventuellement la dérivée seconde qui en représente la courbure (mise en commentaire ici).
' POUR chaque période de cotation de la première à l'avant dernière //i varie donc de 0 à (n-1)
FPRIME4 = B
FixeElemTD(FPRIME4, ZTaille , (ValeurElemTD(B, ZTaille-1) + 2*ValeurElemTD(C, ZTaille-1) + 3*ValeurElemTD(D, ZTaille-1)) )
'Calcul de la dérivée seconde si cela peut intéresser
FSECONDE4 = 2 * C
FixeElemTD(FSECONDE4, ZTaille , (2*ValeurElemTD(C, ZTaille-1) + 6* ValeurElemTD(D, ZTaille-1)) )
' 4- Calculer le momentum à une période de la dérivée première.
' Lisser ce momentum à l'aide de 3 moyennes exponentielles de paramètres P1, P2, P3.
' Calculer la dérivée première lissée et son signal (moyenne exponentielle de paramètre P4)
ZMomentum = FPRIME4 - TRef(FPRIME4, -1)
MM1 = TMME(ZMomentum, 5)
MM2 = TMME(MM1 , 5)
MM3 = TMME(MM2 , 5)
ZMMT = TAbs(ZMomentum)
MM4 = TMME(ZMMT, 5)
MM5 = TMME(MM4 , 5)
MM6 = TMME(MM5 , 5)
DERIVEE1LISSEE = 100 * MM3/MM6
SIGNAL = TMME(DERIVEE1LISSEE, 5)
If Indic = 0 Then
ZResultat = ZBWI
Endif
If Indic = 1 Then
ZResultat = DERIVEE1LISSEE
Endif
If Indic = 2 Then
ZResultat = Signal
Endif
If Indic = 3 Then
ZResultat = FSECONDE4
Endif
SVP = ZResultat
End Function
/////////////////////////////// FIN BIBLIOTHEQUE ///////////////////////////////////////////////////
Ce fût plutôt difficile, car le langage de Platinium ne calcule pas correctement l’expression
ALPHA(0)=3*( VOL(-1) - 2*VOL(0) + VOL(1) )
Il faut décomposer
TOTO(0) = ( VOL(-1) + VOL(1) )
ALPHA(0)=3*(TOTO(0) - 2*VOL(0) )
Le temps de trouver …… Pffffffffffffffff
En conséquence, le code est très décomposé, pas très joli, m’enfin.
J’ai mis le code de Smallcaps dans une bibliothèque pour ne l’écrire qu’une fois.
Il faut ensuite créer des indicateurs dynamiques faisant appel à cette bibliothèque pour chaque courbe à dessiner, du genre
IncludeLib "1215331053:Slope Volatility Predictor"
Result = SVP(TBChart(), 0)
Attention, la ligne IncludeLib "1215331053:Slope Volatility Predictor" sera à remplacer par les références de votre bibliothèque qui n’aura pas les mêmes n°/nom.
Le 0 dans la ligne Result = SVP(TBChart(), 0) précise la courbe à dessiner (voir en fin de bibliothèque). Mettre de 0 à 3 selon la courbe souhaitée. C’est le seul truc un peu élégant, une seule fonction sort plusieurs courbes.
/////////////////////////////// DEBUT BIBLIOTHEQUE ///////////////////////////////////////////////////
function SVP( ZBC as variant, Indic as Integer ) as variant
dim ZTaille as integer ' Taille de l'historique de cours
dim ZTP as variant ' Typical Price
dim ZET as variant ' Ecart Type
dim ZMB as variant ' Moyenne de Bollinger
dim ZBWI as variant ' Bandwidth J. Bollinger ou volatilité normalisée P. Cahen
dim K as integer ' Compteur de boucle
dim ZCalc, ZCalc2, ZCalc3 as Double ' Calcul intermédiaire
dim ZResultat as variant
dim L, U, Z, C, B, D as variant
dim Alpha as variant
dim FPRIME4 as variant
dim DERIVEE1LISSEE as variant
dim FSECONDE4 as variant
dim ZMOMENTUM, ZMMT as variant
dim Signal as variant
dim MM1, MM2, MM3, MM4, MM5, MM6 as variant
' Intialisation des variants
ZResultat = ZBC - ZBC
ZTP = ZResultat
ZET = ZResultat
ZMB = ZResultat
ZBWI = ZResultat
Alpha = ZResultat
L = ZResultat
U = ZResultat
Z = ZResultat
C = ZResultat
B = ZResultat
D = ZResultat
FPRIME4 = ZResultat
FSECONDE4 = ZResultat
Signal = ZResultat
ZMomentum = ZResultat
ZMMT = ZResultat
MM1 = ZResultat
MM2 = ZResultat
MM3 = ZResultat
MM4 = ZResultat
MM5 = ZResultat
MM6 = ZResultat
DERIVEE1LISSEE = ZResultat
' Kalkulations
ZTaille = TailleTD(ZBC) ' Longueur de l'historique
ZTP = TTypPrice(ZBC) ' Typical Price
ZET = TSD(ZTP, 20 ) ' Ecart Type
ZMB = TMMA(ZTP, 20 ) ' Moyenne de Bollinger
ZBWI = (400 * ZET) / ZMB ' Bandwidth J. Bollinger ou volatilité normalisée P. Cahen
'2- Calculer les coefficients A(i), B(i), C(i) et D(i) de la spline cubique libre qui interpole la volatilité relative.
' Les A(i) ne sont pas indispensables à connaître pour calculer la dérivée première de la spline.
' Néanmoins les A(i) sont = VOL(i).
' POUR chaque période de cotation de la première à l'avant dernière //i varie donc de 0 à( n-1)
' ALPHA(i) = 3*VOL(i+1) - 2*VOL(i) + VOL(i-1)
L = TRef(ZBWI,-1)
Z = TRef(ZBWI,+1)
ZResultat = L+Z
Alpha = 3*( ZResultat - 2*ZBWI )
FixeElemTD(L, 1 , 0)
FixeElemTD(U, 1 , 0)
FixeElemTD(Z, 1 , 0)
For K = 2 to (ZTaille-1) ' dans Platinium K=1 désigne le cours le plus ancien
ZCalc = ( 4 - ValeurElemTD(U,(K-1)) )
FixeElemTD(L , K , ZCalc )
ZCalc2 = ( 1 / ZCalc )
FixeElemTD(U , K , ZCalc2 )
ZCalc2 = ( ValeurElemTD(Alpha, K) - ValeurElemTD(Z,(K-1)) )
ZCalc3 = ( ZCalc2 / ZCalc )
FixeElemTD(Z , K , ZCalc3 )
Next
FixeElemTD(L, ZTaille , 1)
FixeElemTD(Z, ZTaille , 0)
FixeElemTD(C, ZTaille , ValeurElemTD(Z,ZTaille) )
' Rétropropagation
' Pour chaque période de cotation de l'avant-dernière à la première //j varie donc de (n-1) à 0
' C(j) = Z(j) - U(j)*C(j+1)
' B(j) = (VOL(j+1) - VOL(j)) - (C(j+1) + 2*C(j)) / 3
' D(j) = (C(j+1) - C(j)) / 3
For K = (ZTaille-1) to 1 step -1
ZCalc = ( ValeurElemTD(U , K) * ValeurElemTD(C, K+1) )
ZCalc2 = ( ValeurElemTD(Z , K ) - ZCalc )
FixeElemTD(C , K , ZCalc2 )
ZCalc = ( ValeurElemTD(ZBWI, K+1) - ValeurElemTD(ZBWI, K) )
ZCalc2 = ( ( ValeurElemTD(C, K+1) + 2*ValeurElemTD(C, K) )/3 )
ZCalc3 = ZCalc - ZCalc2
FixeElemTD(B , K , ZCalc3 )
ZCalc = ( ValeurElemTD(C, K+1) - ValeurElemTD(C, K) )
ZCalc2 = ( ZCalc / 3 )
FixeElemTD(D , K , ZCalc2 )
Next
' 3- Calculer la dérivée première de la spline qui est l'approximation de la pente de la tangente en chaque période //de cotation.
' Et éventuellement la dérivée seconde qui en représente la courbure (mise en commentaire ici).
' POUR chaque période de cotation de la première à l'avant dernière //i varie donc de 0 à (n-1)
FPRIME4 = B
FixeElemTD(FPRIME4, ZTaille , (ValeurElemTD(B, ZTaille-1) + 2*ValeurElemTD(C, ZTaille-1) + 3*ValeurElemTD(D, ZTaille-1)) )
'Calcul de la dérivée seconde si cela peut intéresser
FSECONDE4 = 2 * C
FixeElemTD(FSECONDE4, ZTaille , (2*ValeurElemTD(C, ZTaille-1) + 6* ValeurElemTD(D, ZTaille-1)) )
' 4- Calculer le momentum à une période de la dérivée première.
' Lisser ce momentum à l'aide de 3 moyennes exponentielles de paramètres P1, P2, P3.
' Calculer la dérivée première lissée et son signal (moyenne exponentielle de paramètre P4)
ZMomentum = FPRIME4 - TRef(FPRIME4, -1)
MM1 = TMME(ZMomentum, 5)
MM2 = TMME(MM1 , 5)
MM3 = TMME(MM2 , 5)
ZMMT = TAbs(ZMomentum)
MM4 = TMME(ZMMT, 5)
MM5 = TMME(MM4 , 5)
MM6 = TMME(MM5 , 5)
DERIVEE1LISSEE = 100 * MM3/MM6
SIGNAL = TMME(DERIVEE1LISSEE, 5)
If Indic = 0 Then
ZResultat = ZBWI
Endif
If Indic = 1 Then
ZResultat = DERIVEE1LISSEE
Endif
If Indic = 2 Then
ZResultat = Signal
Endif
If Indic = 3 Then
ZResultat = FSECONDE4
Endif
SVP = ZResultat
End Function
/////////////////////////////// FIN BIBLIOTHEQUE ///////////////////////////////////////////////////
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bravo, bel effort Nacbis...
|
|

christol

(128
msg) ![]()
![]()
![]()
![]()
Bonjour à tous,
Lors du "Duel" du salon de l'AT, Pierre Orphelin a présenté un système à base de régression trigonométrique. L'oscillateur de régression linéaire de graphat donnant de bon résultats, pourquoi pas la regression trigonométrique?
Voici l'info que PO à laissé sur le forum:
"C'est un algorithme qui fait coller au plus près une courbe don l'équation est un polynôme de degré N à celle des cours ( comme la régression linéaire consiste à trouver la droite minimisant la distance des cours à celle ci ( méthode des moindres carrés).
Une régression trigonométrique ( pour répondre à une autre de vos questions) fait la même chose; la courbe n'est alors pas une droite ou n polynôme, mais une courbe de la forme a sin(f1t+ ph1) + cos (f2t+ph2) où f1 et f2 sont les pulsations ( notées habituellement omega et non f , mais j'ai pas ça sur mon clavier) et ph1 et ph2 les phases."
Y a t'il un balèse en prog GRAPHAT que cela tente?
Cordialement, Chris
Lors du "Duel" du salon de l'AT, Pierre Orphelin a présenté un système à base de régression trigonométrique. L'oscillateur de régression linéaire de graphat donnant de bon résultats, pourquoi pas la regression trigonométrique?
Voici l'info que PO à laissé sur le forum:
"C'est un algorithme qui fait coller au plus près une courbe don l'équation est un polynôme de degré N à celle des cours ( comme la régression linéaire consiste à trouver la droite minimisant la distance des cours à celle ci ( méthode des moindres carrés).
Une régression trigonométrique ( pour répondre à une autre de vos questions) fait la même chose; la courbe n'est alors pas une droite ou n polynôme, mais une courbe de la forme a sin(f1t+ ph1) + cos (f2t+ph2) où f1 et f2 sont les pulsations ( notées habituellement omega et non f , mais j'ai pas ça sur mon clavier) et ph1 et ph2 les phases."
Y a t'il un balèse en prog GRAPHAT que cela tente?
Cordialement, Chris
Trade small, don\'t be greedy
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Bonsoir Chctrader,
On y pense depuis quelques temps...
Mais balèze ou pas il faudra attendre que GrapheAT Pro nous permette d'utiliser les lignes trigos SIN et COS dans les règles indicateurs.
Dans une prochaine version peut-être.
On y pense depuis quelques temps...
Mais balèze ou pas il faudra attendre que GrapheAT Pro nous permette d'utiliser les lignes trigos SIN et COS dans les règles indicateurs.
Dans une prochaine version peut-être.
|
|
Jean4713
(1947
msg) ![]()
![]()
![]()
![]()
Chctrader, bonsoir.
On peut tracer des droites de regression linéaires avec grapheAT ?
Ca m'intéresse ! quelqu'un a-t-il posté sur le sujet ?
Merci d'avance.
On peut tracer des droites de regression linéaires avec grapheAT ?
Ca m'intéresse ! quelqu'un a-t-il posté sur le sujet ?
Merci d'avance.
je me trompe
souvent, et le doute m\'habite !  (en province !)
(en province !)
|
|

christol

(128
msg) ![]()
![]()
![]()
![]()
citation :
Citation de Jean4713
Chctrader, bonsoir.
On peut tracer des droites de regression linéaires avec grapheAT ?
Ca m'intéresse ! quelqu'un a-t-il posté sur le sujet ?
Merci d'avance.
Hello man,
Courbe de régression linéaire sur les prix et oscillateur, Oui. mais droite je n'ai pas pas encore vu de développement
Trade small, don\'t be greedy
|
|
smallcaps90
(1022
msg) ![]()
![]()
![]()
![]()
Oui Jean on peut le faire. Mais les outils actuellement dispos dans la version
3.06 nécessitent d'employer un tracé effectué à l'aide du type de courbe "Parabolique".
Et dans les zones où la droite n'est pas tracée il y a des "morceaux" de ce type
de courbe qui sont confondus avec la ligne 0 puisqu'on n'a pas la possibilité
de tracer une droite de longueur limitée sur les cours à l'aide d'un indicateur
actuellement. Et cela écrase les tracés des cours puisque la ligne 0 apparaît
toujours.
Le problème avait en son temps été soumis à Mlog qui je pense va en tenir compte dans une prochaine version tellement l'outil est indispensable.
Voici ce que l'on peut faire pour l'instant,
une ligne de régression linéaire est tracée sur les cours du 45ème au 30ème cours AVANT le dernier (par exemple) :
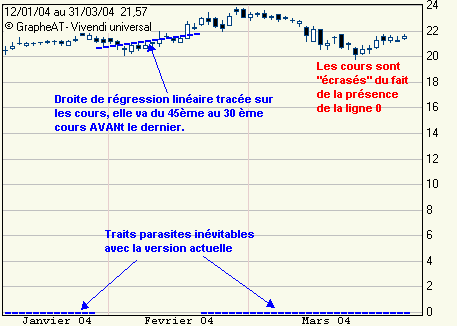
Le problème avait en son temps été soumis à Mlog qui je pense va en tenir compte dans une prochaine version tellement l'outil est indispensable.
Voici ce que l'on peut faire pour l'instant,
une ligne de régression linéaire est tracée sur les cours du 45ème au 30ème cours AVANT le dernier (par exemple) :

édité le : 01-04-2004 19:29:02
|
|

christol

(128
msg) ![]()
![]()
![]()
![]()
citation :
Citation de smallcaps90
Bonsoir Chctrader,
On y pense depuis quelques temps...
Mais balèze ou pas il faudra attendre que GrapheAT Pro nous permette d'utiliser les lignes trigos SIN et COS dans les règles indicateurs.
Dans une prochaine version peut-être.
Merci pour ta réponse,
C'est dommage, Graphat pro est vraiment bien mais montre des limitations. Ben je vais attendre la prochaine version avec impatience. Si mlog pouvait rajouter la possibilité de backtester se serai génial
Trade small, don\'t be greedy
|
|

christol

(128
msg) ![]()
![]()
![]()
![]()
citation :
Citation de smallcaps90
Oui Jean on peut le faire. Mais les outils actuellement dispos dans la version 3.06 nécessitent d'employer un tracé effectué à l'aide du type de courbe "Parabolique". Et dans les zones où la droite n'est pas tracée il y a des "morceaux" de ce type de courbe qui sont confondus avec la ligne 0 puisqu'on n'a pas la possibilité de tracer une droite de longueur limitée sur les cours à l'aide d'un indicateur actuellement. Et cela écrase les tracés des cours puisque la ligne 0 apparaît toujours.
Le problème avait en son temps été soumis à Mlog qui je pense va en tenir compte dans une prochaine version tellement l'outil est indispensable.
Voici ce que l'on peut faire pour l'instant,
une ligne de régression linéaire est tracée sur les cours du 45ème au 30ème cours AVANT le dernier (par exemple) :
T'es vachement doué en prog Graphat smallcaps...
Trade small, don\'t be greedy
|
|
| Sujet : Graphe AT PRo : programmation |